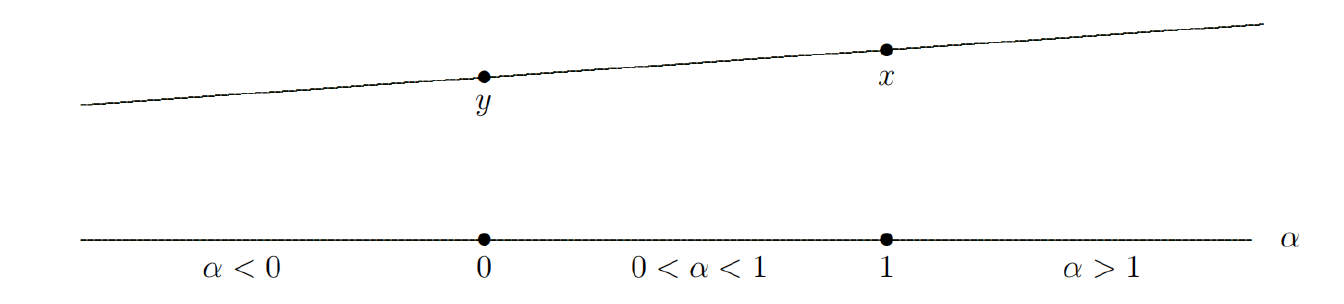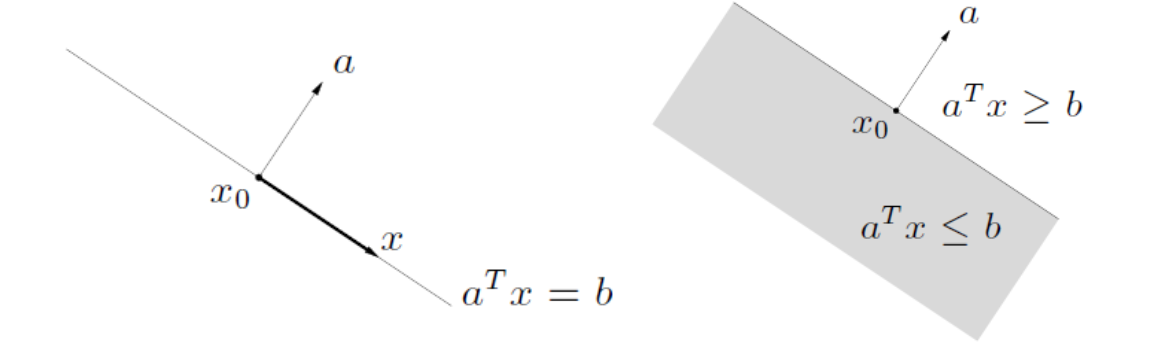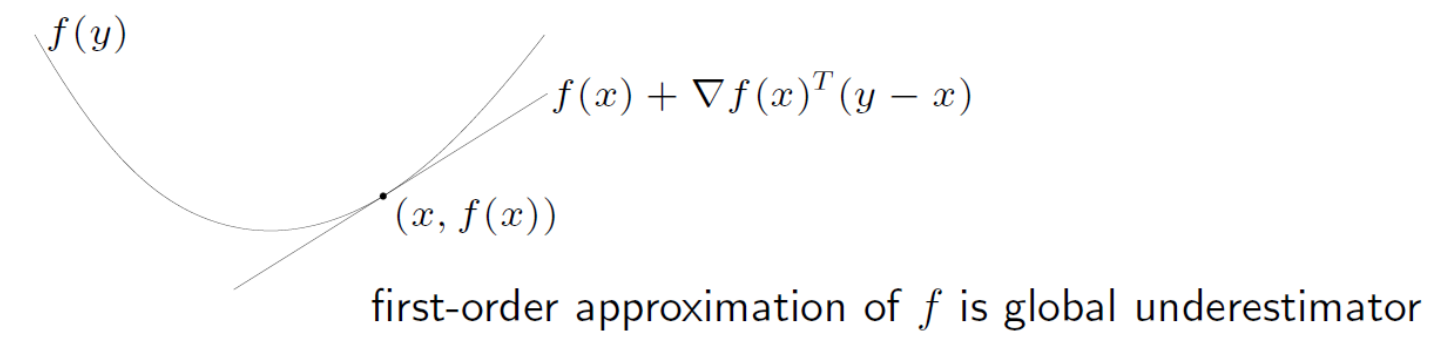最优化理论与方法-引言和预备知识

引言和预备知识

引言

• Optimization
  • 所谓最优化或优化问题通常泛指各类定量决策问题，即如
    何在各种限制约束之下，寻找解决问题的最佳可⾏⽅案，
    使得⼀项或者多项衡量指标达到某种意义上的最优。
  • 这种⼒求达到最优或遵循最优的原则可以说是⼀种⾮常⾃
    然和普遍存在的决策⽬标。通常，我们不仅想找到解决问
    题的可⾏⽅案，还总是希望找到⼀个最好的可⾏⽅案。
  • 甚⾄，这也是宇宙万物的⼀种变化规律。

• 优化的过程

  

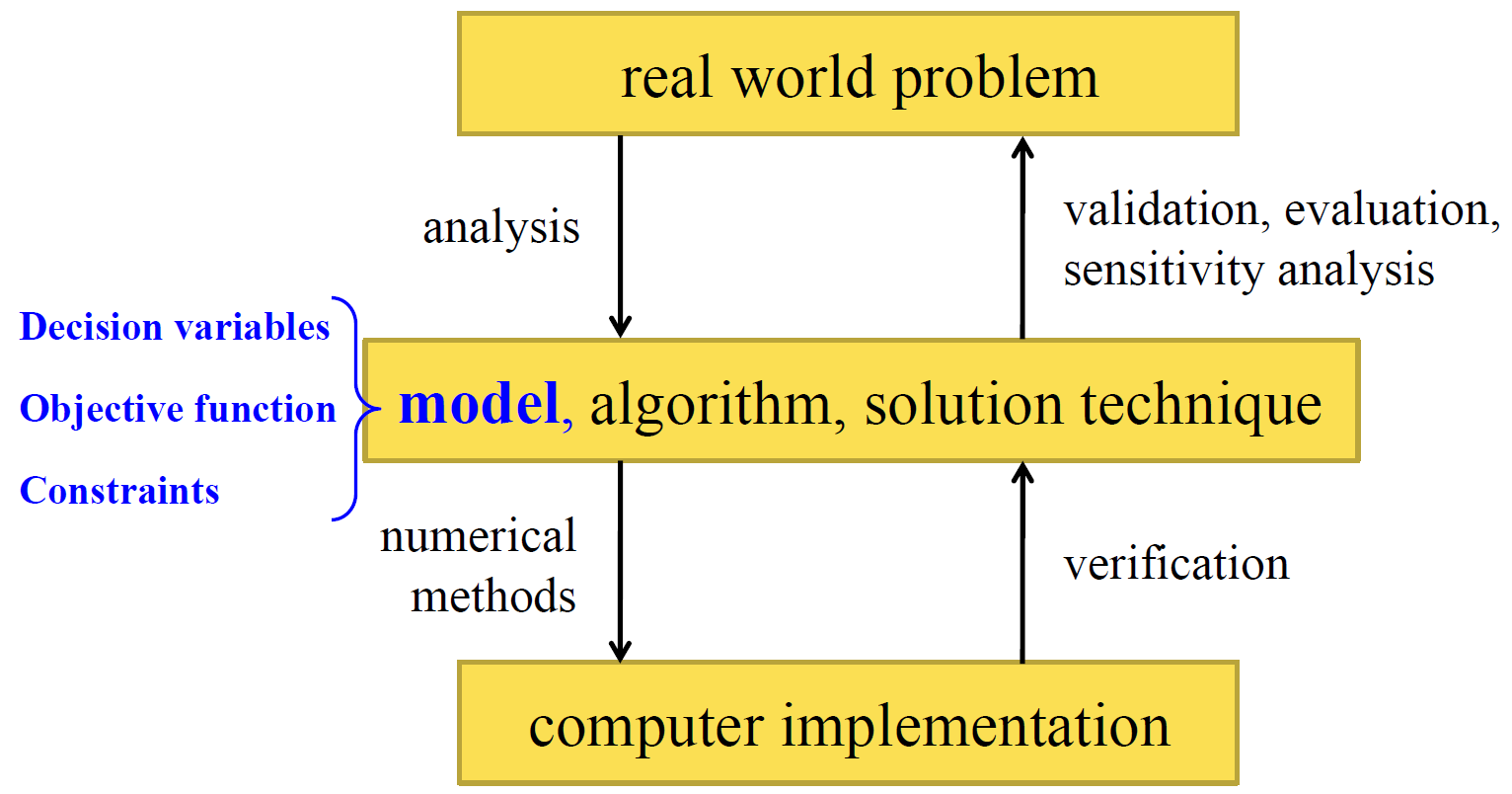
• 数学规划的一般形式：
  

  $$\begin{aligned} &\min (\max) \; f(\mathbf{x}) \\ \text{s.t. } &h_i(\mathbf{x}) = 0, i = 1, \cdots, m \\ & g_j(\mathbf{x}) \leq 0, j = 1, \cdots, r \end{aligned}$$

  其中：

  • $\mathbf{x} = (x_1, \ldots, x_n)^T$：决策变量
  • $f: \mathbb{R}^n \to \mathbb{R}$：目标函数
  • $h_i, g_j: \mathbb{R}^n \to \mathbb{R}, i = 1, \ldots, m, j = 1, \ldots, r$：约束函数
  • $\Omega = \left\{ \mathbf{x} \in \mathbb{R}^n \middle| h_i(\mathbf{x}) = 0, i = 1, \cdots, m; g_j(\mathbf{x}) \leq 0, j = 1, \cdots, r \right\}$：可行域

• 数学规划（Mathematical Programming）的分类

  • 线性 / 非线性 （如：二次规划、凸规划）
  • 光滑 / 非光滑
  • 凸 / 非凸
  • 连续 / 离散 （如：整数规划、混合整数规划）
  • 静态 / 动态 （如：动态规划）
  • 确定性 / 随机性 （如：随机规划、鲁棒优化）
  • 有约束 / 无约束

预备知识

线性代数基础知识

• 向量和矩阵

  • 向量通常用小写字母表示，矩阵通常用大写字母表示。
  • 长度为 $n$ 的实向量空间记为 $\mathbb{R}^n$。
  • $m \times n$ 阶实矩阵空间记为 $\mathbb{R}^{m \times n}$。
  • 若矩阵 $A \in \mathbb{R}^{n \times n}$ 满足 $A = A^T$，则称 $A$ 为对称矩阵。
  • 对称矩阵 $A$ 称为正定（记作 $A \succ 0$），如果
    
    $$x^T A x > 0, \quad \forall\, x \neq 0,\ x \in \mathbb{R}^n$$
  • 若对任意 $x \in \mathbb{R}^n$，有
    
    $$x^T A x \geq 0,$$
    
    则称 $A$ 为半正定（记作 $A \succeq 0$）。

• 范数

  • 一般来说，一个范数 $\|\cdot\|$ 是一个实值函数，满足以下性质：

    • 非负性：对所有 $x$，有 $\|x\| \geq 0$；
    • 正定性：$\|x\| = 0$ 当且仅当 $x = 0$；
    • 齐次性：对任意实数 $\alpha$，有 $\|\alpha x\| = |\alpha| \, \|x\|$；
    • 三角不等式：对所有 $x, y$，有 $\|x + y\| \leq \|x\| + \|y\|$。

  • 对于矩阵范数，以下性质有用但非必需：

    • 相容性（次可乘性）：对任意可乘的矩阵 $X$ 和 $Y$，有
      
      $$\|XY\| \leq \|X\| \, \|Y\|.$$

• 向量范数

  • $l_1$ 范数：
    $\|x\|_1 = \sum_{i=1}^{n} |x_i|$

  • 欧几里得范数（$l_2$ 范数）：
    $\|x\|_2 = \sqrt{x^T x} = \sqrt{\sum_{i=1}^{n} x_i^2}$

  • $l_\infty$ 范数：
    $\|x\|_\infty = \max_{1 \leq i \leq n} |x_i|$

  • $l_p$ 范数（$p \geq 1$）：
    $\|x\|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{\frac{1}{p}}$

  • 加权范数（由正定矩阵诱导）：
    $\|x\|_G = \sqrt{x^T G x}$，其中 $G$ 为对称正定矩阵（即 $G \succ 0$）

  • $l_0$ “范数”：
    $\|x\|_0 =$ 向量中非零元素的个数。

    严格来说，$l_0$ 并不满足范数的齐次性，因此不是真正的范数。

• 向量范数的性质

  • 内积定义：
    向量 $x$ 与 $y$ 的内积记为
    

    $$x \cdot y \equiv x^T y = \sum_{i=1}^n x_i y_i$$

  • Hölder 不等式：
    对任意 $p, q \geq 1$ 满足 $\frac{1}{p} + \frac{1}{q} = 1$，有
    

    $$|x^T y| \leq \|x\|_p \, \|y\|_q$$

  • 对偶范数表示：
    $l_p$ 范数可通过对偶形式表示为
    

    $$\|x\|_p = \max_{\|y\|_q \leq 1} x^T y, \quad \text{其中 } \frac{1}{p} + \frac{1}{q} = 1$$

  • 特例 1：$p = q = 2$（Cauchy–Schwarz 不等式）
    

    $$|x^T y| \leq \|x\|_2 \, \|y\|_2, \quad \|x\|_2 = \max_{\|y\|_2 \leq 1} x^T y$$

  • 特例 2：$p = 1$, $q = \infty$
    

    $$|x^T y| \leq \|x\|_1 \, \|y\|_\infty$$
    
    且
    
    $$\|x\|_1 = \max_{\|y\|_\infty \leq 1} x^T y, \quad \|x\|_\infty = \max_{\|y\|_1 \leq 1} x^T y$$

  • 欧几里得范数与内积的关系：
    

    $$\begin{aligned} \|x\|_2^2 + \|y\|_2^2 &= \|x + y\|_2^2 - 2x^T y \\ &= \|x - y\|_2^2 + 2x^T y \\ &= \frac{1}{2} \left( \|x + y\|_2^2 + \|x - y\|_2^2 \right) \\ &\geq 2\,|x^T y| \end{aligned}$$

  • 向量范数的等价性：
    在 $\mathbb{R}^n$ 中，任意两种向量范数 $\|\cdot\|_*$ 与 $\|\cdot\|_+$ 均满足
    

    $$c_1 \|x\|_+ \leq \|x\|_* \leq c_2 \|x\|_+, \quad \text{其中 } c_1, c_2 > 0 \text{ 为常数}$$
    
    特别地，常见范数之间有如下具体关系：
    
    $$\begin{aligned} &\|x\|_2 \leq \|x\|_1 \leq \sqrt{n}\, \|x\|_2 \\ &\|x\|_\infty \leq \|x\|_2 \leq \sqrt{n}\, \|x\|_\infty \\ &\|x\|_\infty \leq \|x\|_1 \leq n\, \|x\|_\infty \end{aligned}$$

• 矩阵范数

  • 最常用的矩阵范数是由向量范数诱导的范数（也称为算子范数或诱导范数），定义为：
    

    $$\|A\|_p = \max_{x \neq 0} \frac{\|A x\|_p}{\|x\|_p}$$

  • 1-范数（列和范数）：
    

    $$\|A\|_1 = \max_{1 \leq j \leq n} \sum_{i=1}^{m} |a_{ij}|$$
    
    即所有列向量绝对值之和的最大值。

  • 2-范数（谱范数）：
    

    $$\|A\|_2 = \sqrt{\lambda_{\max}(A^T A)}$$
    
    其中 $\lambda_{\max}(A^T A)$ 是 $A^T A$ 的最大特征值。

  • $\infty$-范数（行和范数）：
    

    $$\|A\|_\infty = \max_{1 \leq i \leq m} \sum_{j=1}^{n} |a_{ij}|$$
    
    即所有行向量绝对值之和的最大值。

  • Frobenius 范数（弗罗贝尼乌斯范数）：
    

    $$\|A\|_F = \sqrt{\operatorname{tr}(A^T A)} = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij}^2}$$

  • 迹（Trace）的性质：
    

    $$\operatorname{tr}(A^T B) = \sum_{j=1}^{n} \sum_{i=1}^{m} a_{ij} b_{ij}$$
    
    即两个矩阵对应元素乘积之和（等价于向量化后的内积）。

  • Frobenius 范数的展开公式：
    

    $$\|A + B\|_F^2 = \|A\|_F^2 + \|B\|_F^2 + 2\,\operatorname{tr}(A^T B)$$

  • 正交矩阵（Orthogonal Matrix）的性质：
    若 $Q$ 为正交矩阵，则满足：
    

    $$Q Q^T = Q^T Q = I \quad \text{（因此 } Q^T = Q^{-1} \text{）}$$
    
    并且保持以下范数不变：
    
    $$\|Q A\|_F = \|A\|_F, \quad \|Q A\|_2 = \|A\|_2, \quad \|Q x\|_2 = \|x\|_2$$

• Sherman-Morrison公式

  • 假设原始矩阵 $A \in \mathbb{R}^{n \times n}$，且扰动后的矩阵为 $B = A + uv^T$，其中 $u, v \in \mathbb{R}^n$。

  • 如果已知 $A^{-1}$，如何高效地计算扰动矩阵 $B$ 的逆矩阵？

  • 步骤 1：求解 $(I + uv^T)^{-1}$

    首先，假设矩阵 $(I + uv^T)$ 的逆矩阵形式为 $(I + \rho uv^T)$，则 $\rho$ 的值为：
    

    $$(I + uv^T)(I + \rho uv^T) = I + [1 + \rho(1 + v^T u)]uv^T$$
    
    由此得出：
    
    $$\rho = -\frac{1}{1 + v^T u}$$
    
    因此：
    
    $$(I + uv^T)^{-1} = I - \frac{uv^T}{1 + v^T u}$$

  • 步骤 2：利用上述关系计算 $(A + uv^T)^{-1}$

    其次，利用上述关系，我们有：
    

    $$\begin{aligned} (A + uv^T)^{-1} &= \left(A(I + A^{-1}uv^T)\right)^{-1} \\ &= (I + A^{-1}uv^T)^{-1}A^{-1} \\ &= \left(I - \frac{A^{-1}uv^T}{1 + v^T A^{-1} u}\right)A^{-1} \\ &= A^{-1} - \frac{A^{-1}uv^TA^{-1}}{1 + v^T A^{-1} u} \end{aligned}$$
    
    其中要求 $1 + v^T A^{-1} u \neq 0$。

  • 通过以上步骤，我们可以高效地计算出扰动矩阵 $B = A + uv^T$ 的逆矩阵，而不需要重新进行完整的矩阵求逆运算。这种方法在处理大型矩阵时特别有用，因为它避免了高计算复杂度的直接求逆过程。

• $o$, $O$ 记号

  • 设 $g$ 是一个实变量的实值函数。

  • 记号 $g(x) = O(x)$ 表示当 $x \to 0$ 时，$g(x)$ 趋于零的速度至少与 $x$ 一样快。
    更精确地，存在常数 $K > 0$，使得
    

    $$\left| \frac{g(x)}{x} \right| \leq K \quad \text{当 } x \to 0.$$

  • 记号 $g(x) = o(x)$ 表示 $g(x)$ 趋于零的速度比 $x$ 更快，即
    

    $$\lim_{x \to 0} \frac{g(x)}{x} = 0.$$

  • 在算法分析中，大 $O$ 符号通常用于描述渐近上界（当 $n \to \infty$）：
    

    $$g(n) = O(f(n)) \quad \text{若存在 } C > 0 \text{ 使得 } g(n) \leq C f(n) \text{ 对足够大的 } n \text{ 成立}.$$
    • 例如：$3n^3 + 2n^2 + 5 = O(n^3)$。若算法复杂度为 $O(n^3)$，则输入规模 $n$ 翻倍时，运行时间约增至 8 倍（对大 $n$ 而言）。

  • 在数值分析或泰勒展开中，大 $O$ 和小 $o$ 常用于描述逼近误差（当 $h \to 0$）：
    

    $$g(h) = O(f(h)) \quad \text{若 } |g(h)| \leq C |f(h)| \text{ 当 } h \to 0,$$
    
    
    $$g(h) = o(f(h)) \quad \text{若 } \lim_{h \to 0} \frac{g(h)}{f(h)} = 0.$$

  • 例如，当 $|h| < 1$ 时：
    

    $$\frac{1}{1 - h} = 1 + h + h^2 + h^3 + \cdots = 1 + h + O(h^2),$$
    
    且更精细地，
    
    $$\frac{1}{1 - h} = 1 + h + h^2 + o(h^2).$$

多元函数分析

• 梯度和Hessian矩阵

  • 设 $f$ 是一个 $n$ 元实值函数：
    

    $$f(x) = f(x_1, x_2, \dots, x_n)$$

  • 函数 $f$ 的一阶偏导数组成的向量称为梯度（gradient），记作 $\nabla f(x)$：
    

    $$\nabla f(x) = \left( \frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, \dots, \frac{\partial f(x)}{\partial x_n} \right)^T$$

  • 函数 $f$ 的二阶偏导数组成的矩阵称为Hessian 矩阵（或简称 Hessian），记作 $\nabla^2 f(x)$，其 $(i,j)$ 元素定义为：
    

    $$[\nabla^2 f(x)]_{ij} = \frac{\partial^2 f(x)}{\partial x_i \partial x_j}$$

  • 若 $f$ 的二阶偏导数连续，则 Hessian 矩阵是对称的，即：
    

    $$\frac{\partial^2 f(x)}{\partial x_i \partial x_j} = \frac{\partial^2 f(x)}{\partial x_j \partial x_i}$$

  • 练习：计算以下函数的梯度与 Hessian 矩阵：
    

    $$f(x_1, x_2) = 2x_1^4 + 3x_1^2 x_2 + 2x_1 x_2^3 + 4x_2^2$$
    
    解：
    
    $$\nabla f(x) = \begin{pmatrix} 8x_1^3 + 6x_1 x_2 + 2x_2^3 \\ 3x_1^2 + 6x_1 x_2^2 + 8x_2 \end{pmatrix}, \quad \nabla^2 f(x) = \begin{pmatrix} 24x_1^2 + 6x_2 & 6x_1 + 6x_2^2 \\ 6x_1 + 6x_2^2 & 12x_1 x_2 + 8 \end{pmatrix}$$

  • 练习：计算以下函数的梯度与 Hessian 矩阵：
    

    $$f(x) = \frac{1}{2} x^T Q x - b^T x, \quad \text{其中 } Q \in \mathbb{R}^{n \times n} \text{ 为对称矩阵}$$
    
    解：
    
    $$\nabla f(x) = Qx - b, \quad \nabla^2 f(x) = Q$$

• 雅可比矩阵

  • 考虑向量值函数 $f: \mathbb{R}^n \to \mathbb{R}^m$：
    

    $$f(x) = \begin{pmatrix} f_1(x) \\ f_2(x) \\ \vdots \\ f_m(x) \end{pmatrix}$$

  • 其 Jacobian 矩阵 是一个 $m \times n$ 矩阵，第 $i$ 行第 $j$ 列元素为 $\partial f_i / \partial x_j$，即：
    

    $$J_f(x) = \left[ \frac{\partial f_i}{\partial x_j} \right]$$

  • 练习：计算
    

    $$f(x) = \begin{pmatrix} \sin x_1 + \cos x_2 \\ e^{3x_1 + x_2^2} \\ 4x_1^3 + 7x_1 x_2^2 \end{pmatrix}$$
    
    的 Jacobian。

  • Jacobian 为：
    

    $$\begin{pmatrix} \cos x_1 & -\sin x_2 \\ 3e^{3x_1 + x_2^2} & 2x_2 e^{3x_1 + x_2^2} \\ 12x_1^2 + 7x_2^2 & 14x_1 x_2 \end{pmatrix}$$

• 链式法则

  • 求复合函数导数的法则称为链式法则（chain rule）。

  • 考虑函数 $g(x) = g(x_1, \dots, x_n)$，其中每个变量 $x_i$ 本身是另一组变量 $t_1, \dots, t_m$ 的函数，即 $x_i = x_i(t_1, \dots, t_m)$。

  • 定义复合函数 $h(t) = g(x(t))$，则其梯度满足：
    

    $$\nabla h(t) = \nabla x(t)^T \, \nabla g(x(t))$$
    
    其中 $\nabla x(t)$ 是向量值函数 $x(t)$ 的 Jacobian 矩阵（大小为 $n \times m$），因此 $\nabla h(t) \in \mathbb{R}^m$。

  • 例如：若 $f: \mathbb{R}^n \to \mathbb{R}$ 连续可微，定义 $g(x) = f(Ax - b)$，其中 $A \in \mathbb{R}^{n \times n}$，$b \in \mathbb{R}^n$，则
    

    $$\nabla g(x) = A^T \nabla f(Ax - b)$$

• 方向导数

  • 若 $f$ 连续可微，$p \in \mathbb{R}^n$，则 $f$ 在点 $x$ 沿方向 $p$ 的方向导数定义为：
    

    $$\frac{\partial f(x)}{\partial p} \equiv \lim_{\epsilon \to 0} \frac{f(x + \epsilon p) - f(x)}{\epsilon} = p^T \nabla f(x)$$

  • 为验证该公式，定义辅助函数：
    

    $$\phi(\alpha) = f(x + \alpha p) = f(y(\alpha)), \quad \text{其中 } y(\alpha) = x + \alpha p$$

  • 注意到：
    

    $$\lim_{\epsilon \to 0} \frac{f(x + \epsilon p) - f(x)}{\epsilon} = \lim_{\epsilon \to 0} \frac{\phi(\epsilon) - \phi(0)}{\epsilon} = \phi'(0)$$

  • 由链式法则，
    

    $$\phi'(\alpha) = \sum_{i=1}^n \frac{\partial f(y(\alpha))}{\partial y_i} \, p_i = p^T \nabla f(y(\alpha))$$
    
    因此 $\phi'(0) = p^T \nabla f(x)$，即方向导数等于梯度与方向向量的内积。

• 泰勒级数

  • 泰勒级数（Taylor series）是一种在指定点 $x_0$ 附近近似函数 $f$ 的工具，其近似结果是一个多项式。

  • 只要函数具有足够阶的导数，泰勒级数就可应用，常见用途包括：

    • 在 $x_0$ 附近估计难以直接计算的函数值；
    • 利用近似多项式的导数或积分来估计原函数的导数或积分；
    • 推导求根、优化等数值算法。

  • 对一元函数 $f$（具有 $n$ 阶连续导数），在点 $x_0$ 处的 $n$ 阶泰勒展开为：
    

    $$f(x_0 + p) \approx f(x_0) + p f'(x_0) + \frac{1}{2!} p^2 f''(x_0) + \cdots + \frac{p^n}{n!} f^{(n)}(x_0)$$

  • 前两项给出函数在 $x_0$ 处的切线方程：
    

    $$y = f(x_0) + (x - x_0) f'(x_0)$$

  • 前三项给出二次近似。

  • 对多元函数 $f: \mathbb{R}^n \to \mathbb{R}$，二阶泰勒展开为：
    

    $$f(x_0 + p) = f(x_0) + p^T \nabla f(x_0) + \frac{1}{2} p^T \nabla^2 f(x_0) p + \cdots$$

  • 泰勒级数还有带余项的形式。若取前三项，则：

    • 一元情形：
      
      $$f(x_0 + p) = f(x_0) + p f'(x_0) + \frac{1}{2} p^2 f''(\xi)$$
    • 多元情形：
      
      $$f(x_0 + p) = f(x_0) + p^T \nabla f(x_0) + \frac{1}{2} p^T \nabla^2 f(\xi) p$$
      
      其中 $\xi$ 是介于 $x_0$ 与 $x_0 + p$ 之间的某一点。

  • 通过分析余项的上界，可以评估近似的精度。更高阶项虽可写出，但符号复杂，本课程不作要求。

  • 练习：考虑函数
    

    $$f(x_1, x_2) = x_1^3 + 5x_1^2 x_2 + 7x_1 x_2^2 + 2x_2^3$$
    
    在点 $x_0 = (-2,\, 3)^T$ 处，用二阶泰勒公式近似计算 $f(-1.9,\, 3.2)$。

    已知：
    

    $$f(x_0) = -20, \quad \nabla f(x_0) = \begin{pmatrix} 15 \\ -10 \end{pmatrix}, \quad \nabla^2 f(x_0) = \begin{pmatrix} 18 & 22 \\ 22 & 8 \end{pmatrix}$$

    令 $p = (-1.9,\, 3.2)^T - (-2,\, 3)^T = (0.1,\, 0.2)^T$，则二阶泰勒近似为：
    

    $$f(x_0 + p) \approx f(x_0) + p^T \nabla f(x_0) + \frac{1}{2} p^T \nabla^2 f(x_0) p$$

    计算各项：

    • $p^T \nabla f(x_0) = (0.1)(15) + (0.2)(-10) = 1.5 - 2.0 = -0.5$
    • $p^T \nabla^2 f(x_0) p =
      (0.1,, 0.2)
      \begin{pmatrix} 18 & 22 \ 22 & 8 \end{pmatrix}
      \begin{pmatrix} 0.1 \ 0.2 \end{pmatrix}
      = (0.1)(18\cdot0.1 + 22\cdot0.2) + (0.2)(22\cdot0.1 + 8\cdot0.2)
      = 0.62 + 0.76 = 1.38$

    因此：
    

    $$f(-1.9,\, 3.2) \approx -20 + (-0.5) + \frac{1}{2}(1.38) = -20 - 0.5 + 0.69 = -19.81$$

凸集与凸函数

• 仿射

  • 一个集合 $C$ 称为仿射集（affine set），如果对任意 $x, y \in C$ 和任意实数 $\alpha \in \mathbb{R}$，都有
    

    $$\alpha x + (1 - \alpha) y \in C.$$

  • 当 $x$ 和 $y$ 是 $\mathbb{R}^n$ 中两个不同的点时，所有形如 $z = \alpha x + (1 - \alpha) y$（$\alpha \in \mathbb{R}$）的点构成通过 $x$ 和 $y$ 的直线。

  

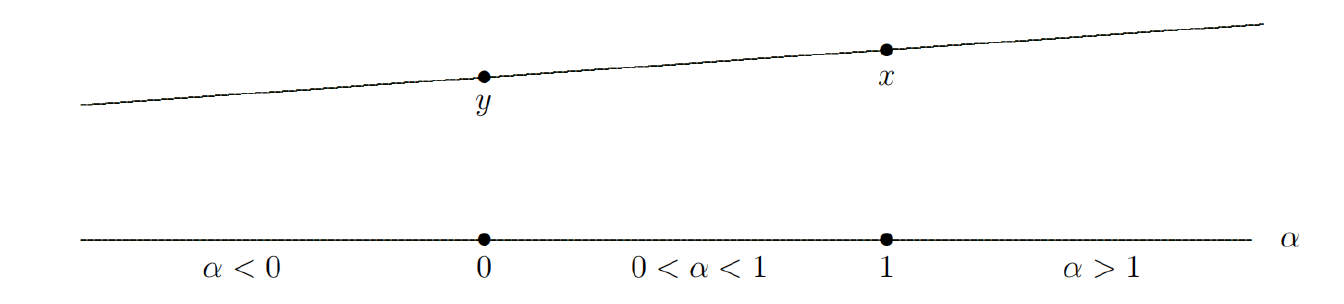
  • 由仿射集的定义可归纳得出：
    若 $C$ 是仿射集，$x_1, \dots, x_k \in C$，且系数满足 $\alpha_1 + \cdots + \alpha_k = 1$，则
    

    $$\alpha_1 x_1 + \cdots + \alpha_k x_k \in C.$$

  • 换句话说，仿射集包含其任意点的仿射组合。

  • 仿射组合（Affine Combination）定义为：
    

    $$y = \sum_{i=1}^{k} \alpha_i x_i, \quad \text{其中 } \sum_{i=1}^{k} \alpha_i = 1.$$

  • 例如，集合 $\{x \mid Ax = b\}$（线性方程组的解集）是一个仿射集。

  • 给定任意集合 $C$，其所有仿射组合构成的集合称为 $C$ 的仿射包（affine hull），记作 $\operatorname{aff} C$，即
    

    $$\operatorname{aff} C = \left\{ \sum_{i=1}^{k} \alpha_i x_i \,\middle|\, x_1, \dots, x_k \in C,\; \sum_{i=1}^{k} \alpha_i = 1,\; k \in \mathbb{N} \right\}.$$

• 凸

  • 一个集合 $C$ 称为凸集（convex set），如果对任意 $x, y \in C$ 和任意 $\alpha \in [0, 1]$，都有
    

    $$\alpha x + (1 - \alpha) y \in C.$$

  • 换句话说，若 $x$ 和 $y$ 属于 $C$，则连接 $x$ 与 $y$ 的线段也完全包含在 $C$ 中。

  

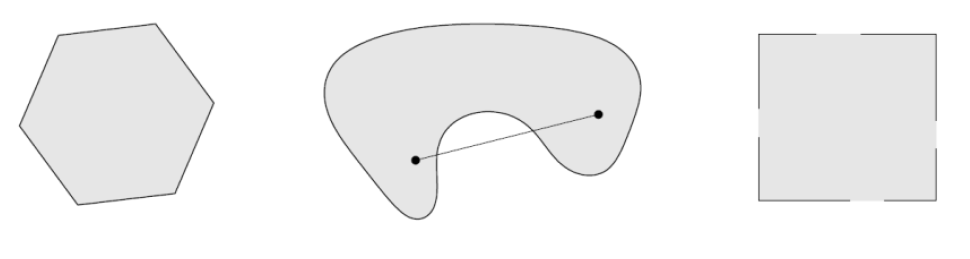
  • 点 $\alpha x + (1 - \alpha) y$（其中 $\alpha \in [0,1]$）称为 $x$ 与 $y$ 的凸组合（convex combination）。

  • 凸组合的一般形式：
    

    $$y = \sum_{i=1}^{k} \alpha_i x_i, \quad \text{其中 } \alpha_i \geq 0,\; \sum_{i=1}^{k} \alpha_i = 1.$$

  • 一个集合是凸集，当且仅当它包含其任意点的所有凸组合。

  • 给定集合 $C$，其所有凸组合构成的集合称为 $C$ 的凸包（convex hull），记作 $\operatorname{conv} C$，即
    

    $$\operatorname{conv} C = \left\{ \sum_{i=1}^{k} \alpha_i x_i \,\middle|\, x_1, \dots, x_k \in C,\; \alpha_i \geq 0,\; \sum_{i=1}^{k} \alpha_i = 1 \right\}.$$

    

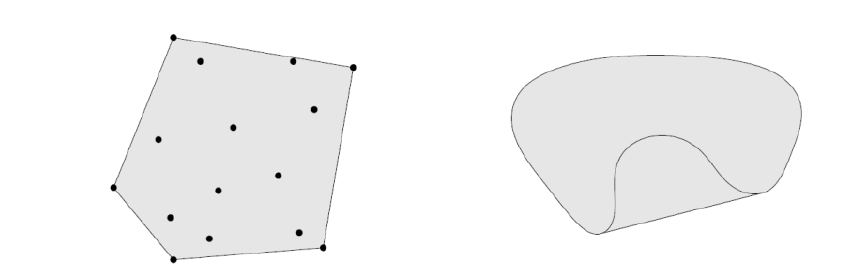
  • 凸集的基本性质：

    • 若 $C_1$ 和 $C_2$ 是凸集，则以下集合也是凸集：
      • $\beta C_1$（标量乘法，$\beta \in \mathbb{R}$），
      • $C_1 + C_2 = \{x + y \mid x \in C_1, y \in C_2\}$（Minkowski 和），
      • $C_1 - C_2 = \{x - y \mid x \in C_1, y \in C_2\}$，
      • $C_1 \cap C_2$（交集，若非空）。
    • 按约定，空集 $\emptyset$ 被视为凸集。

• 超平面和半空间

  • 超平面（Hyperplane）定义为：
    

    $$H = \{ x \mid a^T x = b \}, \quad a \neq 0$$

  • 半空间（Halfspace）分为两类：

    • 闭下半空间：$ H^+ = { x \mid a^T x \leq b } $
    • 闭上半空间：$ H^- = { x \mid a^T x \geq b } $

    其中 $a \neq 0$。

  • 超平面和半空间都是凸集。

    

  • 多面体（Polyhedron）是指有限个半空间与超平面的交集。

    

• 范数球和范数锥

  • 范数球（Norm Ball）：以 $x_c$ 为中心、半径为 $r$ 的范数球定义为
    

    $$B(x_c, r) = \{ x \mid \|x - x_c\| \leq r \}$$

    常见的范数球包括：

    • $l_1$-球：$\{ x \mid \|x - x_c\|_1 \leq r \}$
    • $l_2$-球（欧几里得球）：$\{ x \mid \|x - x_c\|_2 \leq r \}$
    • $l_\infty$-球：$\{ x \mid \|x - x_c\|_\infty \leq r \}$

  • 范数锥（Norm Cone）：
    

    $$\{ (x, t) \mid \|x\|_2 \leq t \} \subseteq \mathbb{R}^{n+1}$$

    其中，欧几里得范数锥也称为二阶锥（Second-Order Cone）或冰激凌锥（Ice-Cream Cone）。

  

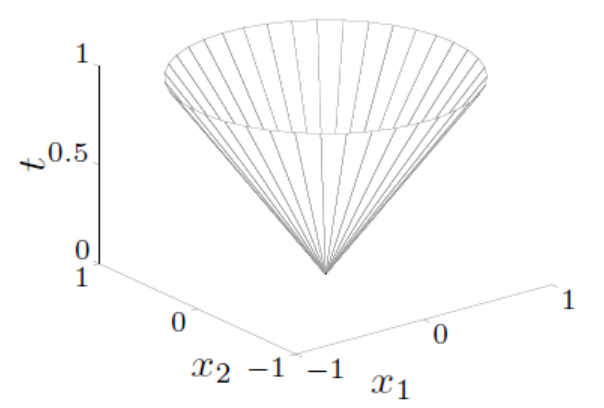
  - 范数球和范数锥都是**凸集**。

• 锥和锥组合

  • 一个集合 $C$ 称为锥（cone），如果对任意 $x \in C$ 和任意 $\theta \geq 0$，都有
    

    $$\theta x \in C.$$

  • 锥组合（Conic Combination，或称非负组合）是指形如
    

    $$x = \theta_1 x_1 + \theta_2 x_2$$
    
    的线性组合，其中 $\theta_1 \geq 0$，$\theta_2 \geq 0$。（可推广到任意有限项）

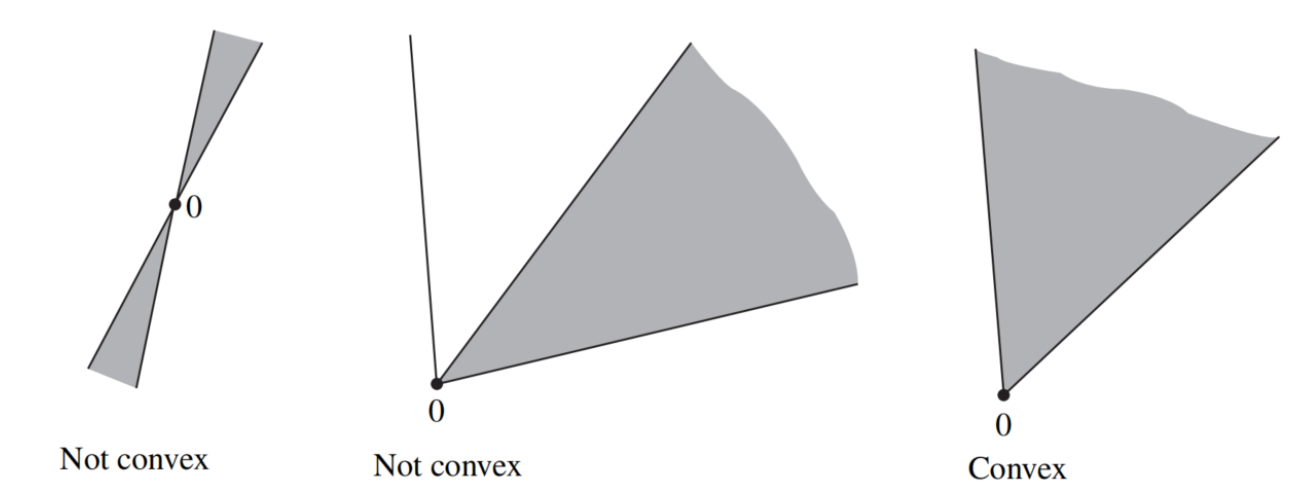
  • 一个集合称为凸锥（convex cone），如果它包含其任意点的所有锥组合。

    

  • 等价地，集合 $C$ 是凸锥，当且仅当对任意 $x, y \in C$ 和任意 $\alpha, \beta \geq 0$，都有
    

    $$\alpha x + \beta y \in C.$$

    

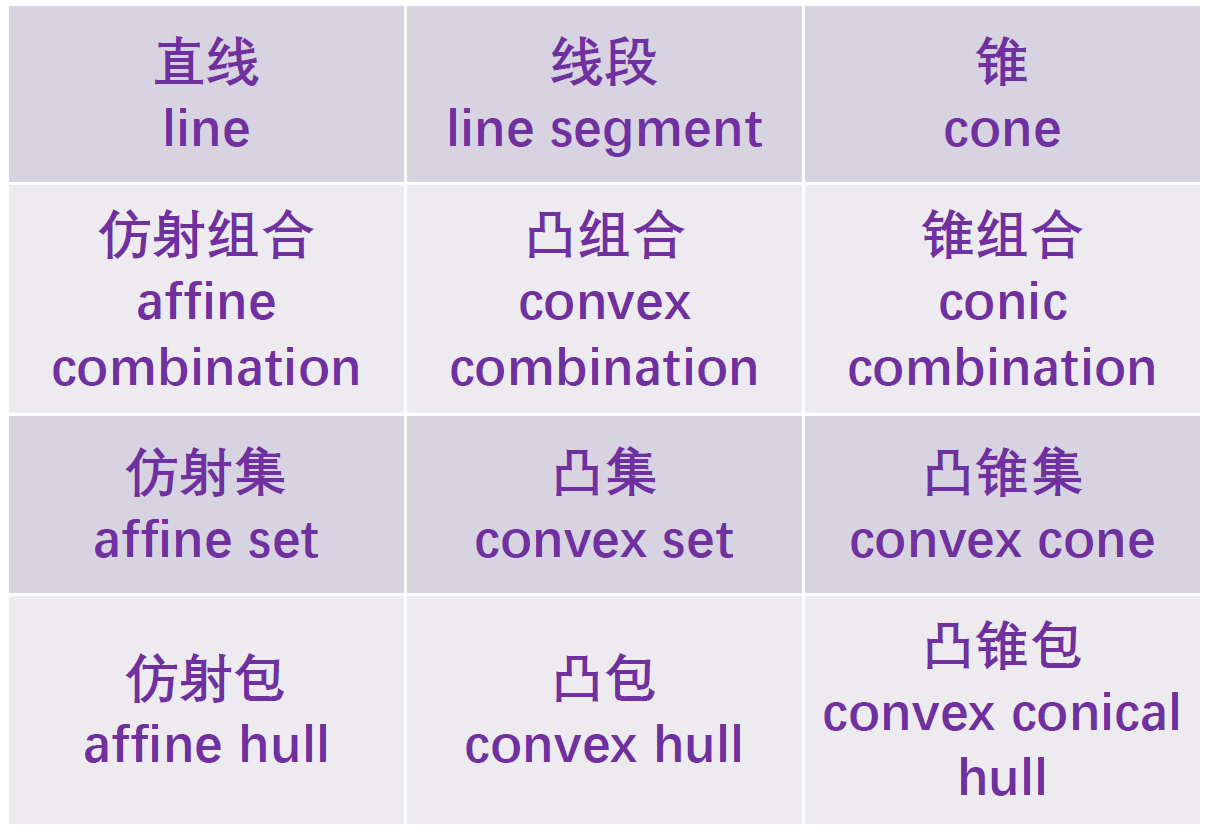
  • 总结

  

• 凸集分离
  设 $D_1, D_2 \subset \mathbb{R}^n$ 为两个非空凸集。若存在非零向量 $a \in \mathbb{R}^n$ 和实数 $\beta$，使得
  

  $$D_1 \subset H^+ = \{ x \in \mathbb{R}^n \mid a^T x \geq \beta \}, \quad D_2 \subset H^- = \{ x \in \mathbb{R}^n \mid a^T x \leq \beta \},$$
  
  则称超平面
  
  $$H = \{ x \in \mathbb{R}^n \mid a^T x = \beta \}$$
  
  分离（separates）集合 $D_1$ 和 $D_2$。

  进一步，如果
  

  $$D_1 \subset H_o^+ = \{ x \in \mathbb{R}^n \mid a^T x > \beta \}, \quad D_2 \subset H_o^- = \{ x \in \mathbb{R}^n \mid a^T x < \beta \},$$
  
  则称超平面 $H$ 严格分离（strictly separates）$D_1$ 和 $D_2$，其中 $H_o^+$ 和 $H_o^-$ 分别表示 $H^+$ 和 $H^-$ 的内部。

• 投影定理
  设 $D \subset \mathbb{R}^n$ 是一个非空闭凸集，点 $y \in \mathbb{R}^n$ 但 $y \notin D$。

  1. 存在唯一最近点：
     存在唯一的点 $\bar{x} \in D$，使得
     

     $$\|\bar{x} - y\| = \inf_{x \in D} \|x - y\|.$$

  2. 最优性条件：
     $\bar{x} \in D$ 是 $y$ 到 $D$ 的最近点，当且仅当
     

     $$(x - \bar{x})^T (\bar{x} - y) \geq 0, \quad \forall x \in D.$$

  • 证明：

    (1) 存在唯一性

    • 距离函数 $\|x - y\|$ 在闭集 $D$ 上连续，且 $D$ 非空 → 最小值可达（存在性）。
    • 因为 $\|x - y\|^2$ 是严格凸函数，而 $D$ 是凸集 → 最小值点唯一。

    (2) 最优性条件

    • 必要性：若 $\bar{x}$ 是最近点，则对任意 $x \in D$，线段上的点 $z_\theta = \bar{x} + \theta(x - \bar{x}) \in D$（由凸性）。
      函数 $\theta \mapsto \|z_\theta - y\|^2$ 在 $\theta = 0$ 处最小，其导数 $\geq 0$，即
      

      $$\frac{d}{d\theta}\Big|_{\theta=0} \|z_\theta - y\|^2 = 2(x - \bar{x})^T(\bar{x} - y) \geq 0.$$

    • 充分性：若 $(x - \bar{x})^T(\bar{x} - y) \geq 0$ 对所有 $x \in D$ 成立，则
      

      $$\|x - y\|^2 = \|\bar{x} - y\|^2 + 2(x - \bar{x})^T(\bar{x} - y) + \|x - \bar{x}\|^2 \geq \|\bar{x} - y\|^2,$$
      
      所以 $\bar{x}$ 确实是最接近 $y$ 的点。

• 点与凸集分离定理
  设 $D \subset \mathbb{R}^n$ 是一个非空闭凸集，点 $y \in \mathbb{R}^n$ 但 $y \notin D$。则存 在非零向量 $a \in \mathbb{R}^n$ 和实数 $\beta$，使得
  

  $$a^T x \leq \beta < a^T y, \quad \forall x \in D.$$
  
  这表示存在超平面
  
  $$H = \{ x \in \mathbb{R}^n \mid a^T x = \beta \}$$
  
  严格分离点 $y$ 与集合 $D$：整个集合 $D$ 位于超平面的一侧（含边界），而点 $y$ 严格位于另一侧。

  • 证明：
    设 $D \subset \mathbb{R}^n$ 是非空闭凸集，$y \notin D$。
    由投影定理，存在唯一的 $\bar{x} \in D$ 使得 $\|\bar{x} - y\|$ 最小，且满足
    

    $$(x - \bar{x})^T(\bar{x} - y) \geq 0, \quad \forall x \in D.$$

    整理不等式得：
    

    $$x^T(y - \bar{x}) \leq \bar{x}^T(y - \bar{x}), \quad \forall x \in D.$$

    令 $a = y - \bar{x}$。因为 $y \neq \bar{x}$，所以 $a \neq 0$。
    上式变为：
    

    $$a^T x \leq a^T \bar{x}, \quad \forall x \in D.$$

    又因为 $a^T y = a^T(\bar{x} + a) = a^T \bar{x} + \|a\|^2 > a^T \bar{x}$，
    所以对所有 $x \in D$ 有：
    

    $$a^T x \leq a^T \bar{x} < a^T y.$$

    令 $\beta = a^T \bar{x}$，则
    

    $$a^T x \leq \beta < a^T y, \quad \forall x \in D,$$
    
    即超平面 $\{x \mid a^T x = \beta\}$ 严格分离点 $y$ 与集合 $D$。

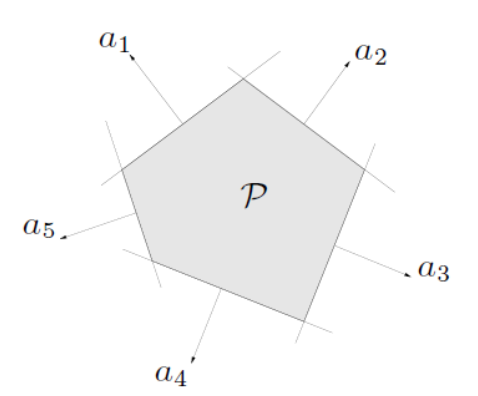
• 支撑超平面

  • 设 $D \subset \mathbb{R}^n$ 是非空集合，点 $\bar{x} \in \partial D$（即 $\bar{x}$ 是 $D$ 的边界点）。
    若存在非零向量 $a \in \mathbb{R}^n$，使得
    

    $$D \subset H_{\bar{x}}^+ = \{ x \in \mathbb{R}^n \mid a^T(x - \bar{x}) \geq 0 \}$$
    
    或
    
    $$D \subset H_{\bar{x}}^- = \{ x \in \mathbb{R}^n \mid a^T(x - \bar{x}) \leq 0 \},$$
    
    则称超平面
    
    $$H_{\bar{x}} = \{ x \in \mathbb{R}^n \mid a^T(x - \bar{x}) = 0 \}$$
    
    为集合 $D$ 在点 $\bar{x}$ 处的一个支撑超平面。

  • 若 $D$ 是非空凸集，则在其每一个边界点处都存在至少一个支撑超平面。

• 两个凸集的分离定理

  • 设 $D_1, D_2 \subset \mathbb{R}^n$ 为两个非空凸集，且 $D_1 \cap D_2 = \emptyset$。
    则存在一个超平面分离 $D_1$ 与 $D_2$，即存在非零向量 $a \in \mathbb{R}^n$，使得
    

    $$a^T x \leq a^T y, \quad \forall\, x \in \overline{D}_1,\; y \in \overline{D}_2.$$

  • 证明：
    令 $D = D_1 - D_2 = \{ x - y \mid x \in D_1,\; y \in D_2 \}$。
    由于 $D_1$ 和 $D_2$ 均为凸集，其差集 $D$ 也是凸集；又因 $D_1 \cap D_2 = \emptyset$，故 $0 \notin D$。

    考虑闭包 $\overline{D}$，它仍是凸集且不包含原点。由点与闭凸集的分离定理，存在非零向量 $a \in \mathbb{R}^n$，使得
    

    $$a^T z \leq 0, \quad \forall\, z \in \overline{D}.$$

    对任意 $x \in \overline{D}_1$、$y \in \overline{D}_2$，有 $z = x - y \in \overline{D}$，代入得
    

    $$a^T (x - y) \leq 0 \;\Longrightarrow\; a^T x \leq a^T y,$$
    
    即所求分离不等式成立。

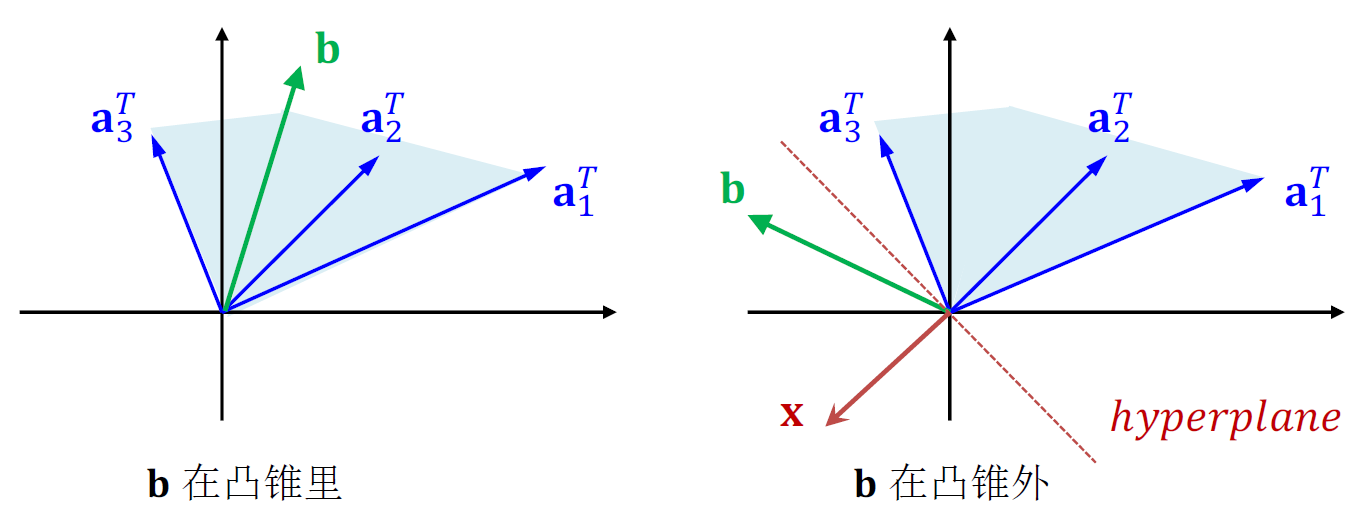
• Farkas 引理
  设 $A \in \mathbb{R}^{m \times n}$，$b \in \mathbb{R}^n$。则以下两个系统中有且仅有一个有解：

  • 系统 (1)：
    

    $$A^T y = b, \quad y \geq 0$$

  • 系统 (2)：
    

    $$Ax \leq 0, \quad b^T x > 0$$

    其中 $x \in \mathbb{R}^n$，$y \in \mathbb{R}^m$。

  • 几何理解：

  

• 凸函数

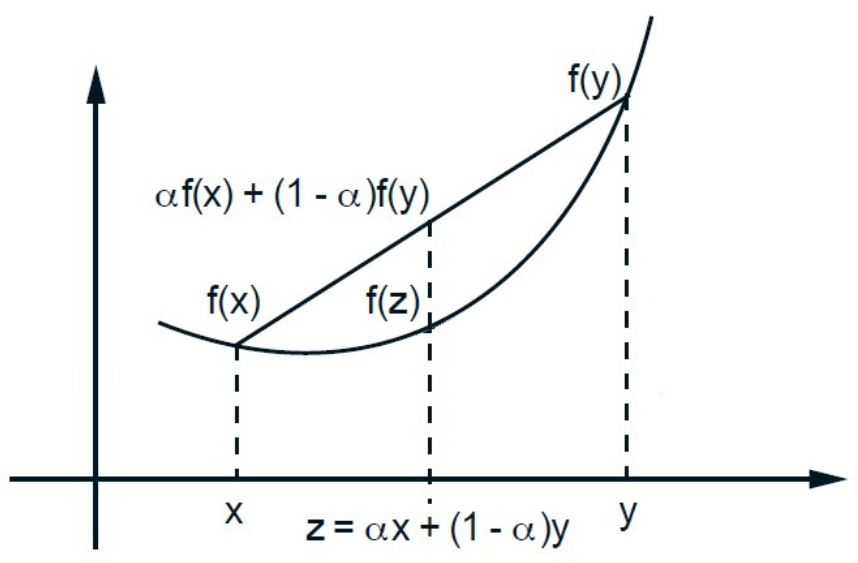
  • 设 $C \subset \mathbb{R}^n$ 为凸集，函数 $f: C \to \mathbb{R}$ 称为 凸函数，如果对任意 $x, y \in C$ 和任意 $\alpha \in (0,1)$，都有
    

    $$f(\alpha x + (1 - \alpha) y) \leq \alpha f(x) + (1 - \alpha) f(y).$$

  • 若上述不等式对所有 $x \neq y \in C$ 和 $\alpha \in (0,1)$ 严格成立，即
    

    $$f(\alpha x + (1 - \alpha) y) < \alpha f(x) + (1 - \alpha) f(y),$$
    
    则称 $f$ 为 严格凸函数。

  • 凸函数（或严格凸函数）的相反数称为 凹函数（或严格凹函数）。

  • 线性函数既是凸函数，也是凹函数。

  

  • 一阶条件（适用于定义在凸集 $C$ 上的可微函数 $f$）：

    • 函数 $f$ 在 $C$ 上是凸函数，当且仅当
      

      $$f(y) \geq f(x) + \nabla f(x)^T (y - x), \quad \forall\, x, y \in C.$$

    • 函数 $f$ 在 $C$ 上是严格凸函数，当且仅当
      

      $$f(y) > f(x) + \nabla f(x)^T (y - x), \quad \forall\, x, y \in C,\; x \neq y.$$

      

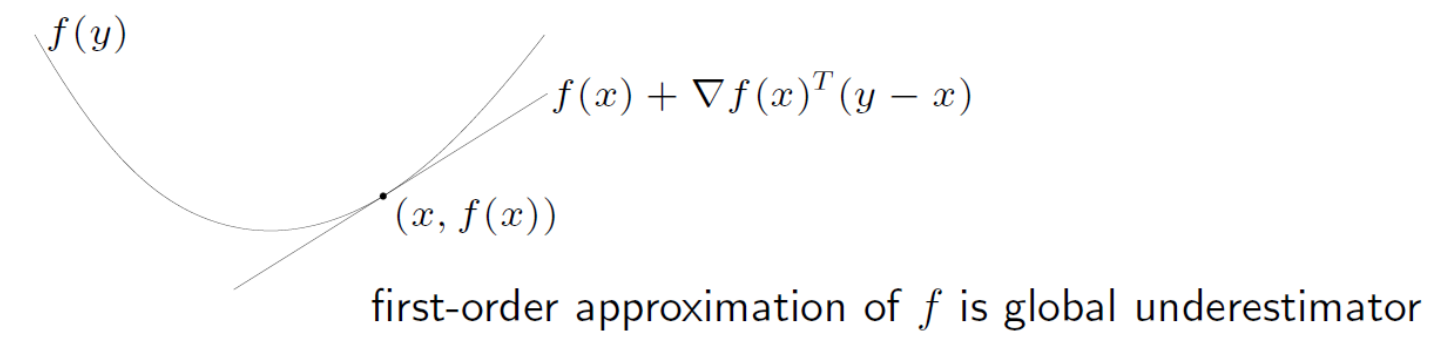
  该条件表明：凸函数在其任意点处的一阶泰勒展开是全局下界；严格凸时，该下界在其他点严格成立。

  • 二阶条件（适用于定义在开凸集 $C \subset \mathbb{R}^n$ 上的二阶连续可微函数 $f$）：

    • 函数 $f$ 在 $C$ 上是凸函数，当且仅当其 Hessian 矩阵半正定，即
      

      $$\nabla^2 f(x) \succeq 0, \quad \forall\, x \in C.$$

    • 若对所有 $x \in C$，Hessian 矩阵正定，即
      

      $$\nabla^2 f(x) \succ 0,$$
      
      则 $f$ 是严格凸函数。
      （注：这是严格凸的充分条件，但非必要条件。）

  • 一维凸函数的例子：

    • 指数函数：$f(x) = e^{a x}$，其中 $a \in \mathbb{R}$，在 $\mathbb{R}$ 上是凸函数。

    • 幂函数：$f(x) = x^{\alpha}$，定义在 $x > 0$ 上，当 $\alpha \geq 1$ 或 $\alpha \leq 0$ 时为凸函数。

    • 负对数函数：$f(x) = -\ln x$，在 $x > 0$ 上是凸函数。

    • 负熵函数：$f(x) = x \ln x$，在 $x > 0$ 上是凸函数（约定 $0 \ln 0 = 0$ 可将其连续延拓至 $x = 0$）。

    • 需要注意的是，并非所有凸函数都是可微的。

      • 一个简单的不可微凸函数例子是绝对值函数：
        
        $$f(x) = |x| = \begin{cases} x, & \text{若 } x \geq 0, \\ -x, & \text{若 } x < 0. \end{cases}$$
        
        该函数在 $x = 0$ 处不可导，但在整个 $\mathbb{R}$ 上是凸函数。

  • 上方图

    • 设 $f$ 是定义在集合 $S \subset \mathbb{R}^n$ 上的实值函数。
      函数 $f$ 的上镜图（epigraph）定义为
      

      $$\operatorname{epi} f = \left\{ (x, \mu) \in \mathbb{R}^{n+1} \,\middle|\, x \in S,\; \mu \geq f(x) \right\}.$$
      
      它表示 $\mathbb{R}^{n+1}$ 中位于函数图像之上或恰好在图像上的所有点构成的集合。

    • 设 $S \subset \mathbb{R}^n$ 是非空凸集，则函数 $f: S \to \mathbb{R}$ 是凸函数 当且仅当 其上镜图 $\operatorname{epi} f$ 是 $\mathbb{R}^{n+1}$ 中的凸集。

    这一定理建立了凸函数与凸集之间的等价关系，常用于证明某些函数的凸性。

  • 水平集 (Level Set)
    假设 $f$ 是定义在 $L \subset \mathbb{R}^n$ 上的实值函数。对于任意 $\alpha \in \mathbb{R}$，集合

    $$L_\alpha = \{ x \mid f(x) \leq \alpha, \; x \in L \}$$

    称为函数 $f$ 的 $\alpha$ 水平集。

    若 $L \subset \mathbb{R}^n$ 是非空凸集，且 $f$ 是定义在 $L$ 上的凸函数，则对任意 $\alpha \in \mathbb{R}$，水平集 $L_\alpha$ 是一个凸集。

    • 水平集是所有满足 $f(x) \leq \alpha$ 的点 $x$ 构成的集合。
    • 如果函数 $f$ 是凸函数，并且其定义域是凸集，则该函数的所有水平集也是凸集。这为我们判断某些集合是否为凸提供了一种方法。

• 凸规划

  • 凸规划（Convex Programming）是指如下形式的优化问题：
    

    $$\min_{x \in S} f(x)$$
    
    其中，可行域 $S \subset \mathbb{R}^n$ 是一个凸集，目标函数 $f$ 在 $S$ 上是凸函数。

  • 示例：
    考虑问题
    

    $$\begin{aligned} \min \quad & f(x) \\ \text{s.t.} \quad & g_i(x) \geq 0, \quad i = 1, \dots, m \end{aligned}$$
    
    若目标函数 $f(x)$ 是凸函数，且每个约束函数 $g_i(x)$ 是凹函数，则该问题是凸规划。

  • 理由：
    由于 $g_i$ 是凹函数，集合 $\{x \mid g_i(x) \geq 0\}$ 是凸集（凹函数的上水平集为凸集）。
    多个凸集的交集仍是凸集，因此可行域
    

    $$S = \bigcap_{i=1}^m \{x \mid g_i(x) \geq 0\}$$
    
    是凸集。结合 $f$ 为凸函数，该问题满足凸规划的定义。

• 可行性

  • 考虑如下形式的约束条件：
    

    $$\begin{aligned} g_i(x) &= 0, && i \in E \quad \text{（等式约束）} \\ g_i(x) &\geq 0, && i \in I \quad \text{（不等式约束）} \end{aligned}$$

  • 满足所有约束条件的点称为可行点（feasible point）。
    所有可行点构成的集合称为可行域（feasible region）或可行集。

  • 在一个可行点 $\bar{x}$ 处，不等式约束 $g_i(x) \geq 0$ 被称为：

    • 起作用（active / binding），如果 $g_i(\bar{x}) = 0$（即该点位于约束边界上）；
    • 不起作用（inactive / nonbinding），如果 $g_i(\bar{x}) > 0$（即该点位于约束内部）。

  • 所有等式约束在任意可行点处均视为起作用。

  • 在可行点 $\bar{x}$ 处的起作用集（active set）定义为在该点处所有起作用约束（包括全部等式约束和满足 $g_i(\bar{x}) = 0$ 的不等式约束）的下标集合。

  • 所有满足至少一个不等式约束起作用（即 $g_i(x) = 0$ 对某个 $i \in I$ 成立）的可行点，构成可行域的边界。

  • 其余的可行点（即所有不等式约束均严格成立：$g_i(x) > 0$ 对所有 $i \in I$）称为可行域的内点。

  • 对于无约束优化问题，可行集 $S$ 即为整个 $\mathbb{R}^n$。

• 最优性

  • 若点 $x^*$ 满足
    

    $$f(x^*) \leq f(x), \quad \forall\, x \in S,$$
    
    则称 $x^*$ 为函数 $f$ 在集合 $S$ 上的全局最小值点（global minimizer）。

  • 若进一步满足
    

    $$f(x^*) < f(x), \quad \forall\, x \in S \text{ 且 } x \neq x^*,$$
    
    则称 $x^*$ 为 $f$ 在 $S$ 上的严格全局最小值点（strict global minimizer）。